Boat Dock
Boat docks are structures extending alongshore or out from a shore into a body of water, to which boats can be moored. As facilities, they occur as collections along the water adjacent to villages, towns and cities. They also occur single at points where a road or route reaches but does not pass over a semi-navigable or navigable river, or intersects with a lake. Boat docks only occur in hexes where a hammer symbol is present.
Boat docks are small in size, ranging from 6 to 12 ft. wide and 8 to 20 ft. long. When built on a river, they run parallel to the shore; upon a lake, they extend outward from the shore. Boat docks do not occur in water deeper than 12 ft. The primary benefit of a dock is for the loading and unloading of goods by service boats, which may or may not also carry passengers. Boat docks are not sufficiently secure or wide enough to load or unload ships greater than 5 tons in size, which require a quay. Depending upon the sort of route and hex type, docks may also enable passage across a river where a ferry does not exist.
In very cold climates, when a river freezes, all use of the boat dock ceases until the river is again clear of ice. At best, the dock provides sufficient means to support 1-3 persons.
Contents
River Ports
Although the main transfer of goods in towns and cities occur at quays or wharves, boat docks for individuals proliferate along the water's edge along both sides of a river or along a body of water. In towns and cities, freelance boathandlers operating lighters, pramms, launches or dories are available to carry passengers across a river for a fee of 2 c.p. per trip, per point of river. Wait time is normally 2-16 minutes. Freight costs 5 c.p. per hundred lbs. Boats are available even if the river is bridged.
Villages have a single boathandler available to shuttle travellers across a river, and this is nearly always no more than a rowboat. Costs are the same, but wait time is extended to 3-30 minutes. Village boathandlers are more likely to deny passage to those whose character seems threatening or unseemly.
Use the rules below for Boat Types and Passengers.
Interrupted Routes
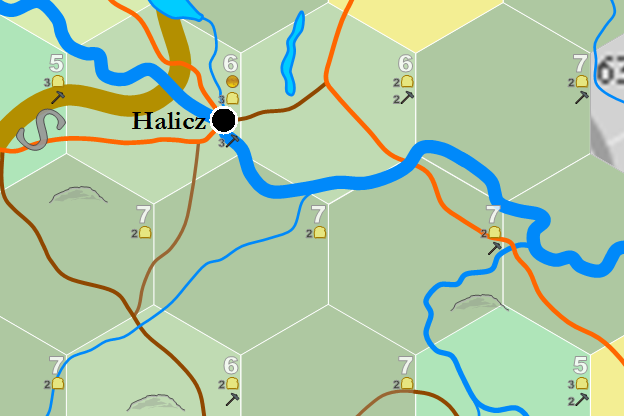
The image shows an example of a cobblestone road (orange) that's interrupted by a water course, the Dniester River southeast of Halicz in Poland. The Dniester is "5 pts." wide at this point, as indicated by the size the river appears on the map. On one side of the interruption, we have a type-6 hex with 2 hammer symbols; on the other side, we have a type-7 with 1 hammer. Note that we can see an example further east where the same road passes over a 2 pt. tributary. This indicates a bridge.
Directly south of Halicz, we can also see a dirt road (dark brown) that's interrupted by a 1 pt. tributary. An instance like this doesn't indicate a boat dock, because a stream of 1 pt. isn't considered "semi-navigable." A stream of that size can be forded, though with some difficulty, as they offer many places along their course where the water is less than 3 ft. deep.
There are three matters to be determined regarding interrupted routes: the likelihood of finding a boat there; the type of boat being found there; and the willingness of that boat to take on passengers.
At the point where the boat dock occurs, there will be a thorp or hamlet located there, regardless of the hex type. Therefore, there are people there to tell the party when the next boat is expected and what sort of boat it is.
Docking
| Route | Colour | Wait Time (hour) |
|---|---|---|
| High Road | red | 0-1 |
| Low Road | pink | 0-3 |
| Cobblestone Road |
orange | 1-6 |
| Dirt Road | dark brown | 1-16 |
| Cart Track | light brown | 1-40 |
| Cart Path | green | 1-100 |
Docking describes the likelihood, or how much time needs to pass, before a traveller should expect to find a boat arriving, waiting or ready to load at that boat dock. When calculating wait times, only daylight hours are counted. Thus is could be that a boat set to arrive in 96 hours might take as long as six or seven days to appear. Also, if a boat is due in three hours, but the sun will set in two, the boat won't arrive until the next morning. The DM may unilaterally choose to count every day as having 16 daylight hours, or he or she might choose to actually calculate the number of daylight hours according to the season.
The initial die roll mustn't create a bell curve ... since there's an equal chance that a boat might arrive at any hour within the time indicated. Once the arrival time is known, further arrivals at that point can be predicted by adding the maximum total time for that route type, plus-or-minus 0-3 hours.
- For example, the party arrives at the interrupted cobblestone road shown on the map. A d6 is rolled, indicating that the party must wait 5 hours before a boat arrives. The next boat after that, the "second" boat, will arrive 6 hours later. Here, we can apply a bell curve, so for the next boat we roll 2d4, minus 5 and applying that to the expected six hours. Rolling a 7(-5), we add 2 to 6 and the second boat arrives 8 hours after the first. Obviously, this knowledge is withheld until the boat appears.
Where boat docks occur on high roads, assume the continuous presence of available boats; the wait time is therefore in reference to how long the traveller must wait until the boat departs. This might also apply, sometimes, to low road boat docks, though often no boat is present. With all other route-based boat docks, assume a minimum of 1 hour wait before departure occurs.
Boat Types
However long it takes for a boat to arrive, what arrives is also important. This is determined by the number of hammer symbols for the boat dock's hex.
| No. Hammers |
Boat Type |
|---|---|
| 1 | Dory |
| 2 | Pramm |
| 3 | Launch |
| 4 | Lighter |
| 5 | Scow |
| 6 | Heavy Barge |
Boats, when they arrive, are never empty; they travel up and down the river, delivering and collecting goods and serving as a messenger service ... as well as a source for news of the world abroad. These boats, regardless of size, are never empty, being typically 20-80% full. This means that even if the boat is able to take on passengers, with small boats there's likely not to be enough room to take on a whole party and their possessions. Details about travel aboard boats is described below
- Dories are very light, similar in some ways to modern rowboats, with a capacity of only 1,000 lbs., with a length of 11 ft. The draft is just 5 inches. It's not possible to load an animal onto a dory unless the animal can be lifted into the boat. It must then be kept calm. Most horses would exceed weight limits in any case.
- Pramms should not be confused with the modern utility dinghy, being shallow-draft vessels that are commonly flat-bottomed vessels but not necessarily so. A pramm has a capacity of 1 ton, or 2,000 lbs, with a length of 14 ft. The draft is 7 inches. They're strong enough to allow a horse or cow to step down into them, but there's a 1 in 20 chance that the vessel's integrity might give, requiring constant bailing thereafter — at a cost of 2-5 g.p. to the owner to repair the boat. Nonetheless, the owner may take the risk if 5 g.p. is entrusted to him before the attempt is made, which is then returned if all is well.
- Launches resemble a ship's boat, with 2 tons capacity, possessing a single-stepped mast, with rings for hoisting. The vessel is 18 feet long, with a 6 ft. beam. The draft is 9 inches. The boat can take even warhorses aboard without trouble.
- Lighters resemble a small pinnace or barque, with fixed mast, with a lateen rig. Lighters have a capacity of 4 to 6 tons, ranging between 24 and 29 ft. long. They keep a crew of 2 to 3 boathandlers. They have a draft of 1 to 1½ ft., with a centerboard can be removed. On 2 pt. rivers, replace with launch.
- Scows are lengthy flat-bottomed shells with loads covered with canvas. 60 ft. in length, they carry up to 20 tons of cargo. They have a draft of only 1 ft. They include a captain, cook and 4 polers. If rowed, as occurs on most slow moving tropical or sub-tropical rivers, seats are provided for 8-20 oarsmen. They include quarters. On 3 pt. or smaller rivers, replace with lighter.
- Heavy barges are like scows, though they are 80 ft. in length and carry a cargo of 50 tons. They have a draft of 16 inches. They include a captain, cook and 5 polers, or 10-26 oarsmen. On 3 pt. or smaller rivers, replace with lighter.
Note that the largest possible vessel may not be the one that arrives. For example, if a boat dock's hex had 3 hammers, then the next arrival might be a dory, a pramm or a launch. The DM may give an equal chance of each, or may weight the random result for the largest possible ship (say, on a d6, a 1 is a dory, 2-3 is a pramm and 4-6 is a launch).
Passengers
Unless the hex include a gold coin symbol, a vessel arriving at a boat dock won't take passengers up or down river under any circumstances. The cost is 1 c.p. per coin number, per 6-mile hex to be travelled, per passenger. Thus, in the case of Halicz in the map shown above, which has 1 coin, the cost to take a journey from there equals 1 c.p. per person per 6-mile hex. There is a 50/50 chance that any given boat will be going up or down river, which the players much accept as the possible destination.
The next stop must equal the number of hammers where the boat was boarded. Thus, the launch that stops at Halicz (3 hammers), won't stop again until it reaches a stop of equal or greater value. If a pramm were boarded at the point where the river is interrupted in the example above, where the boat dock has 2 hammers, the next stop upstream would be Halicz; downstream, it would be the next boat dock in a hex with 2 hammers, whether a village, town, city or isolate boat dock.
Should no more destinations in a given direction be possible, then the boat's journey is predetermined. If no other destination of the right type exists anywhere on the river, then the destination is the river's mouth, where goods are transshipped to another vessel that waits there.
Freight costs 5 c.p. per 200 lbs. per 6-mile hex, counting 1 hex as a minimum.
Begging Rides
Travellers caught at a boat dock where no gold coin exists, may yet wangle a ride from a boathandler across the river, if not along it. This requires a successful charisma check by the character with the lowest charisma. The cost is established as 4 c.p. per trip, determined by how many people and how much is carried. Freight is counted at 5 c.p. per hundred pounds.
See also,
The Adventure
Type-7 Hex