Difference between revisions of "Hex Group"
Tao alexis (talk | contribs) |
Tao alexis (talk | contribs) |
||
| Line 6: | Line 6: | ||
== Distributing Groups == | == Distributing Groups == | ||
| − | Beginning with the infrastructure number for a 20-mile hex, the seven prime hexes, or "group," are randomly assigned an order from 1 to 7. These are then allotted, in order, an amount of infrastructure according to their order. The hexes have a designation starting at the top | + | Beginning with the infrastructure number for a 20-mile hex, the seven prime hexes, or "group," are randomly assigned an order from 1 to 7. These are then allotted, in order, an amount of infrastructure according to their order. The hexes have a designation starting at the top right and moving in a circle, with the last hex in the centre, as Hex-A, Hex-B, Hex-C and so on. A new random order is assigned to the seven hexes each time infrastructure is distributed, ensuring a unique pattern for every group. |
When assigning infrastructure, the original number is divided according to powers of 2: 2<sup>0</sup>, 2<sup>1</sup>, 2<sup>2</sup>, 2<sup>3</sup> and so on... while assigning empty hexes zero infrastructure. That is, | When assigning infrastructure, the original number is divided according to powers of 2: 2<sup>0</sup>, 2<sup>1</sup>, 2<sup>2</sup>, 2<sup>3</sup> and so on... while assigning empty hexes zero infrastructure. That is, | ||
| − | :* 0 = 0 infrastructure (0-IN) — type-8 (see "[[Hex Group#Hex Type|Hex Types]]" below) | + | :* 0 = 0 infrastructure (0-IN) — [[Type-8 Hex|type-8]] (see "[[Hex Group#Hex Type|Hex Types]]" below) |
| − | :* 2<sup>0</sup> = 1-IN — type-7 | + | :* 2<sup>0</sup> = 1-IN — [[Type-7 Hex|type-7]] |
| − | :* 2<sup>1</sup> = 2-IN — type-6 | + | :* 2<sup>1</sup> = 2-IN — [[Type-6 Hex|type-6]] |
| − | :* 2<sup>2</sup> = 4-IN — type-5 | + | :* 2<sup>2</sup> = 4-IN — [[Type-5 Hex|type-5]] |
| − | :* 2<sup>3</sup> = 8-IN — type-4 | + | :* 2<sup>3</sup> = 8-IN — [[Type-4 Hex|type-4]] |
| − | :* 2<sup>4</sup> = 16-IN — type-3 | + | :* 2<sup>4</sup> = 16-IN — [[Type-3 Hex|type-3]] |
| − | :* 2<sup>5</sup> = 32-IN — type-2 | + | :* 2<sup>5</sup> = 32-IN — [[Type-2 Hex|type-2]] |
| − | :* 2<sup>6</sup> = 64-IN — type-1 | + | :* 2<sup>6</sup> = 64-IN — [[Type-1 Hex|type-1]] |
The total infrastructure must be divided into these seven options, plus zero, when distributing that infrastructure into the subordinate hex group of seven prime hexes... recognising that multiple combinations are possible for most infrastructure totals above 1. '''For example''', 3 infrastructure divided into seven hexes may be, according to the assigned order of the hexes. These combinations might be either 2-1-0-0-0-0-0 or 1-1-1-0-0-0-0. For a total infrastructure of 8-IN, there are nine possible combinations, and for 42-IN, there are twenty-nine possible combinations. The chance of any specific combination occurring, regardless of the total, is always equal. This means that for a total of 42-IN, any of the 29 possible distributions has an equal probability of being selected. | The total infrastructure must be divided into these seven options, plus zero, when distributing that infrastructure into the subordinate hex group of seven prime hexes... recognising that multiple combinations are possible for most infrastructure totals above 1. '''For example''', 3 infrastructure divided into seven hexes may be, according to the assigned order of the hexes. These combinations might be either 2-1-0-0-0-0-0 or 1-1-1-0-0-0-0. For a total infrastructure of 8-IN, there are nine possible combinations, and for 42-IN, there are twenty-nine possible combinations. The chance of any specific combination occurring, regardless of the total, is always equal. This means that for a total of 42-IN, any of the 29 possible distributions has an equal probability of being selected. | ||
[[File:Hex Generator.jpg|right|490px|thumb|Hex generator]] | [[File:Hex Generator.jpg|right|490px|thumb|Hex generator]] | ||
| − | A [https://docs.google.com/spreadsheets/d/1OD6XRL4yDHfS5N0F7SFIspfWpy72bYB2/edit#gid=1269951915 generator] in | + | A [https://docs.google.com/spreadsheets/d/1OD6XRL4yDHfS5N0F7SFIspfWpy72bYB2/edit#gid=1269951915 generator] in Excel has been created to automatically perform both tasks simultaneously: assigning the order of the prime hexes and randomly distributing infrastructure across them. The result is expressed as 'types,' ranging from type-8 to type-1." |
| + | |||
| + | The hex types are resulting are then assigned, in order, to the hexes labelled 1st, 2nd, 3rd, etcetera. In the example shown, for 12 total infrastructure, the type-4 is placed in Hex D, the type-5 in Hex G, and the remaining five type-8 distributed into the remaining hexes. | ||
| + | |||
| + | |||
Revision as of 19:54, 31 January 2025
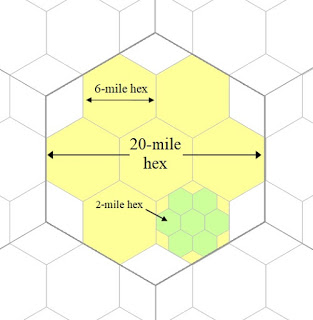
Hex groups are a designation for a constituency of 9 hexes that fit conviently inside a larger hex — seven prime hexes and six diamonds each representing ⅓ of a hex. This allows a hex to be subdivided for the purpose of randomly assigning portions of a 20-mile hex's infrastructure number, providing a collection of "hex types" numbering from type-1 to type-8. While the game world is mapped in 20-mile hexes for estimating travel times for player characters and the movement of goods and services, 6-mile hexes as determined through hex groups are used to provide more detailed information for the purpose of running the game setting.
This means of subdividing hexes can be used to expand details of the game world as desired, for 6-mile hexes can similarly be subdivided into 2-mile hexes, which can be reduced progressively into "plough hexes" (1,304 yards), ¼-mile hexes (434 yards), blocks (145 yards) and sub-blocks (48 yards). This allows us to map virtually anything.
Distributing Groups
Beginning with the infrastructure number for a 20-mile hex, the seven prime hexes, or "group," are randomly assigned an order from 1 to 7. These are then allotted, in order, an amount of infrastructure according to their order. The hexes have a designation starting at the top right and moving in a circle, with the last hex in the centre, as Hex-A, Hex-B, Hex-C and so on. A new random order is assigned to the seven hexes each time infrastructure is distributed, ensuring a unique pattern for every group.
When assigning infrastructure, the original number is divided according to powers of 2: 20, 21, 22, 23 and so on... while assigning empty hexes zero infrastructure. That is,
The total infrastructure must be divided into these seven options, plus zero, when distributing that infrastructure into the subordinate hex group of seven prime hexes... recognising that multiple combinations are possible for most infrastructure totals above 1. For example, 3 infrastructure divided into seven hexes may be, according to the assigned order of the hexes. These combinations might be either 2-1-0-0-0-0-0 or 1-1-1-0-0-0-0. For a total infrastructure of 8-IN, there are nine possible combinations, and for 42-IN, there are twenty-nine possible combinations. The chance of any specific combination occurring, regardless of the total, is always equal. This means that for a total of 42-IN, any of the 29 possible distributions has an equal probability of being selected.
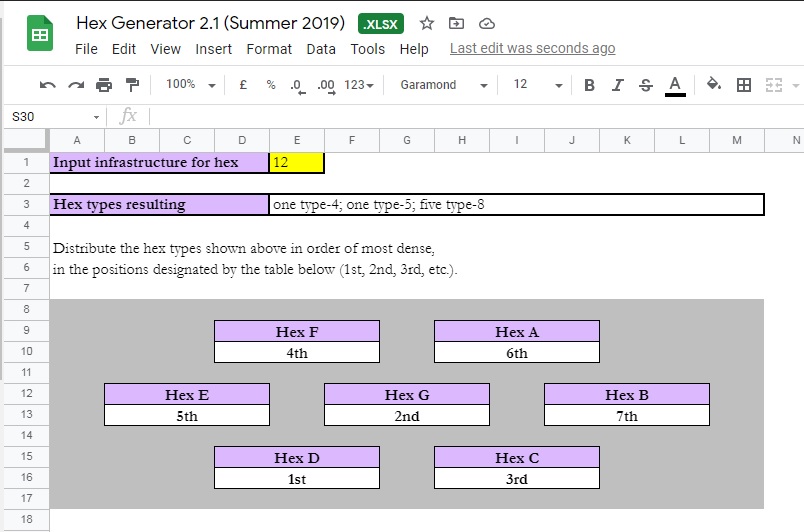
A generator in Excel has been created to automatically perform both tasks simultaneously: assigning the order of the prime hexes and randomly distributing infrastructure across them. The result is expressed as 'types,' ranging from type-8 to type-1."
The hex types are resulting are then assigned, in order, to the hexes labelled 1st, 2nd, 3rd, etcetera. In the example shown, for 12 total infrastructure, the type-4 is placed in Hex D, the type-5 in Hex G, and the remaining five type-8 distributed into the remaining hexes.
This describes the means by which the infrastructure of the 20-mile hex is distributed among the seven prime, or whole six-mile hexes forming the hex group. Infrastructure numbers range from zero (no habitation or infrastructure at all) into the thousands — though for distributing groups, an infrastructure of 448 or more means the hex group is fully civilised.
A hex group with zero infrastructure has seven type-8 hexes; "type-8" being the least civilised type. Every six-mile hex in this group is wild, without any human structures or facilities. If adjacent to human culture, a hex like this would be considered "hinterland" — visited regularly by hunters and gatherers, but with nothing more developed than an animal-made trail.
1 point of infrastructure would mean the hex group has six type-8 hexes and one type-7 hex. This type-seven hex, 6.67 miles across, has one two-mile hex within it that's civilised. The remainder of the 2 mile hexes, and most of the six-mile hex, is counted as hinterland. A single point of infrastructure is very little. It's understood, then, that the "hex type" is determined by how many two-mile hexes within that six-mile hex are civilised. None equals a type-8 hex; one equals a type-7; two equals a type-6 and so on, until if every two-mile hex is civilized, the six-mile hex is a type-1. Conversely, if there are no wild hexes, that's a type-1; and for each wild hex that's added, the hex becomes type-2 (includes one wild hex), type-3 (includes two), type-4 (includes three) and so on. While this counting systems seems confusing at first, it quickly becomes second-nature.
Patterns
The image shown indicates the possible hex distributions for each type of hex, with black indicating a wild hex and white indicating a hex that's civilised. Type-1 and type-8 hexes can only have one possible pattern, or distribution: every 2-mile hex is of one type or the other.
Type-2 and type-7 hexes may have the single civilised/wild hex in the center of the group, or as one of the six outer hexes. There are seven permutations for where the exact distribution may be, but there are only 2 patterns: in the middle or on the outside.
The remaining hex types continue become more elaborate, with type-3 mirroring type-6 and type-4 mirroring type-5. Altogether, there are no more than 26 patterns, but as these patterns are turned clockwise and interface with the permutations created by adjacent hexes, they form an interesting and functional mosaic of civilized hexes.
Random Distribution
While 1 point of infrastructure creates a type-7 hex, it requires 2 points of infrastructure to create hex that is type-6. Therefore, distributing 2 infrastructure among a hex group might create either TWO type-7 hexes or ONE type-6. Which is rolled randomly, with an equal chance for each. More civilised types progressively require more infrastructure to generate: at least 4 pts to make a type-5, 8 pts to make a type-4 and so on. A type-1 hex cannot occur with less than a minimum of 64 infrastructure pts, and seven type-1 hexes would cost 448 total. This explains the number needed to obtain a fully civilised 20-mile hex.
A complete list of possible group combinations occuring at specific infrastructure totals for a hex, can be found here. Because the number of possible combinations is considerable, manually interpreting the die roll for each level of infrastructure quickly, and as often as it needs doing, is impractical. Therefore, a generator has been created that can be used on google sheets or downloaded. The file includes various flotsam and jetsam that can be ignored.
By inserting the infrastructure number in the yellow box and hitting return, the hex types resulting will be generated, explaining how many of each type. Seven boxes then show how these hexes can be arranged randomly. In the example shown, the single type-4 hex would be located in "Hex D," which has the box below reading, "1st." Thereafter, the single type-5 shown is placed in the "2nd" hex, which is "Hex G," the center hex. The remaining hexes are all type-8, which are placed in the other five hexes.
If the hex were partly water, so that Hex D had no land or perhaps an inconsequential sliver of land, then the type-4 hex would be placed in the next suitable hex in order, from 2nd to 3rd to 4th and so on. This allows a quick adjustment for odd circumstances that arise in mapping, without needing to create a complicated program to account for such things.
See Mapmaking